Waarom statistiek niet te vertrouwen is?

Onlangs verscheen het nieuwe boek van Ben Orlin met de titel ‘Wiskunde is overal‘ (Uitgeverij Lannoo). In het boek neemt hij de lezer mee op een meeslepende reis in de wonderlijke wereld van de wiskunde.

Op de website van Scientias.nl wordt als voorproefje het hoofdstuk dat handelt over statistiek uitgelicht.

“De interessantste kritiek op statistiek richt zich niet op de oneerlijkheid van de statisticus, maar op de wiskunde zelf,” aldus Orlin. “We kunnen de waarde van statistieken opkrikken door hun onvolmaaktheid te begrijpen, door te zien wat elke statistiek wil zeggen en wat ze doelbewust vergeet.” Hoogste tijd dus voor een lesje in statistiek (en haar serieuze tekortkomingen).

Het gemiddelde
Hoe werkt het? Tel alle beschikbare data bij elkaar op. Deel het totaal door het aantal data.
Wanneer gebruik je het? Het gemiddelde vervult een basisbehoefte in de statistiek: je bepaalt de ‘centrale tendens’ van een groep. Hoe lang is dat basketbalteam? Hoeveel ijsjes verkoop je per dag? Hoe heeft de klas het bij het proefwerk gedaan? Als je een hele populatie met één waarde probeert samen te vatten, is het gemiddelde een logische eerste kandidaat.
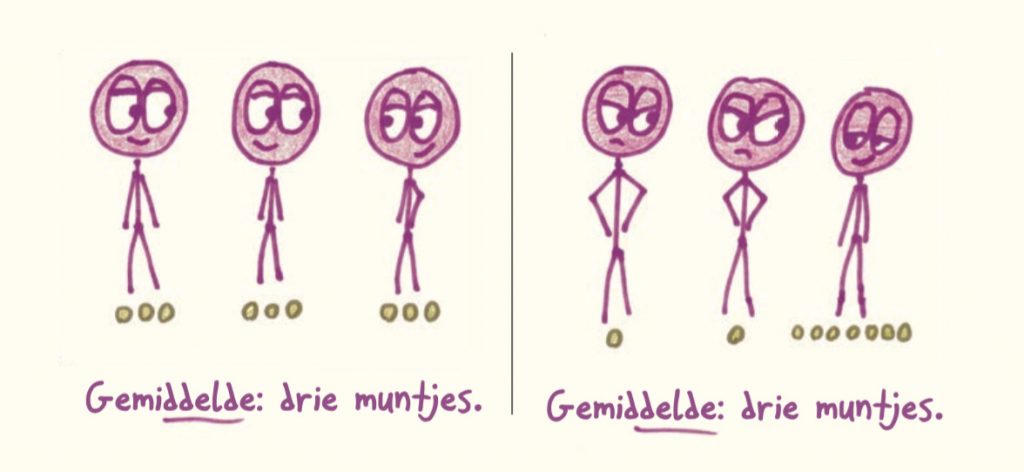
Wat mankeert eraan? Het gemiddelde kijkt alleen maar naar het totaal en het aantal mensen dat bijdraagt aan dat totaal. Als je wel eens een piratenschat heb verdeeld, ken je het probleem. Er zijn veel manieren om de buit te verdelen. Hoeveel heeft elk individu bijgedragen? Iedereen evenveel of één persoon heel veel? Als ik een hele pizza eet en jij niets krijgt, is het dan eerlijk om te zeggen dat wij ‘gemiddeld’ een halve pizza hebben gegeten? Je kunt je tafelgasten vertellen dat de ‘gemiddelde mens’ één eierstok en één teelbal heeft, maar sterft het gesprek dan niet een pijnlijke dood? (Ja, ik heb het geprobeerd.) Mensen maken zich druk om de verdeling, niet om het gemiddeld

Gelukkig zijn gemiddelden wel gemakkelijk te berekenen. Stel dat je toetscijfers 87, 88 en 96 zijn (dit vak is een eitje voor je!). Wat is dan het gemiddelde? Overbelast je neuronen niet met optellen en delen; maak een nieuwe verdeling. Neem zes punten van je laatste toets; geeft drie ervan aan de eerste en twee aan de laatste toets. Nu heb je scores van 90, 90 en 90 en nog één punt over. Als je dat eenzame puntje onder de drie toetsen verdeelt, kom je op een gemiddelde van 90,33, zonder je hersenen te kraken.

Ook andere statistische grootheden worden aan de hand van goed gekozen voorbeelden uitgelegd: mediaan, modus, percentiel, variantie, correlatiecoëfficiënt.

Lees het volledige artikel op de website scientias.nl via deze link